
注意!!浏览本文前务必手动刷新一下页面,否则里面的公式无法渲染!!这是因为签入的代码没有考虑到PJAX的可用性,所以导致无刷新加载后JS失效,正在想办法解决中...
🔰前言和基础知识
今天正好空余时间较足,所以看一节超长函授应该不成问题吧😂(虽然还是超级懒,哈哈哈。)但是3个小时实在是太烧脑力,我还是留一部分给明天消化吧。之后特此整理笔记,顺便测试一下Typecho输入公式的可行方法。
原来是依靠插入图片来输入复杂的数学公式,今天新加入了一个Typecho的数学公式插件。本来还想说插件蛮好用加载很快,但是紧接着发现和我的博客主题并不兼容,出现了许多非常棘手的文章功能失灵,甚至连正常的内容换行都没办法用了,只好放弃并卸载。
之后我又看到了这篇文章,照着直接修改主题代码就可以支持公式使用了,之后也发现并没有影响我的其他内容显示。之后我做笔记就直接插入$\LaTeX{}$就好咯~ 如果之后在网页显示上有什么其他问题爆出来,请留言或发邮件告诉一下!
圆锥曲线基础知识
首先圆锥曲线可以略分为:椭圆、双曲线、抛物线。
它们的部分性质如下,这些是作答解析大题的基础。
标准方程(X轴为焦点):$\frac{x^2}{a^2}+\frac{y^2}
{b^2}=1\left(a>b>0\right)$
焦点:$F_1(-c,0),F_2(c,0)$
标准方程(Y轴为焦点):$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1\left(a>b>0\right)$
焦点:$F_1(0,-c),F_2(0,c)$
长轴长:$2a$,短轴长:$2b$,焦距:$|F_1F_2|=2c$
a,b,c的关系:$c^2=a^2-b^2$
离心率:$\mathrm{e}=\frac{c}{a}=\sqrt{1-\frac{b^{2}}{a^{2}}}\left(0<\mathrm{e}<1\right)$
准线方程:$x=\pm\frac{a^{2}}{c}$,切线方程:$\frac{x_0x}{a^2}+\frac{y_0y}{b^2}=1$
通径:$|AB|=\frac{2b^{2}}{a}$
标准方程(X轴为焦点):$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$
焦点:$F_1(-c,0),F_2(c,0)$
标准方程(Y轴为焦点):$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1(a>0,b>0)$
焦点:$F_1(0,-c),F_2(0,c)$
实轴长:$2a$,虚轴长:$2b$,焦距:$|F_1F_2|=2c$
a,b,c的关系:$c^2=a^2+b^2$
离心率:$\mathrm{e}=\frac{c}{a}=\sqrt{1+\frac{b^{2}}{a^{2}}}(\mathrm{e}>1)$,准线方程:$x=\pm\frac{a^2}{c}$
渐近线(X轴焦点):$y=\pm\frac{b}{a}x$
渐近线(Y轴焦点):$y=\pm\frac{a}{b}x$
切线方程(X轴焦点):$\frac{x_0x}{a^2}-\frac{y_0y}{b^2}=1$
切线方程(Y轴焦点):$\frac{x_0x}{b^2}-\frac{y_0y}{a^2}=1$
通径:$|AB|=\frac{2b^{2}}{a}$
设点设线的方法
一句废话总结:看哪个方便设哪个就好。
如果其他动点的表示需要依赖一个点,就设点入手;如果动点的表示依赖直线方程的话,设线即可。
设点坐标解题的思路
例题(北京 2016):已知$P$是椭圆$C:$$\frac{x^{2}}{4}+y^{2}=1$上一点,直线$PA$与$y$轴交于点$M,$ 直线$PB$与$x$轴交于点$N.$ 求证:$|AN|\cdot|BM|$为定值.
由于$N$和$M$需要的直线都过点$P$,用$P$坐标表示$PM,PN$直线后可以依据$X=0,Y=0$推出$M,N$坐标。
具体的解答过程: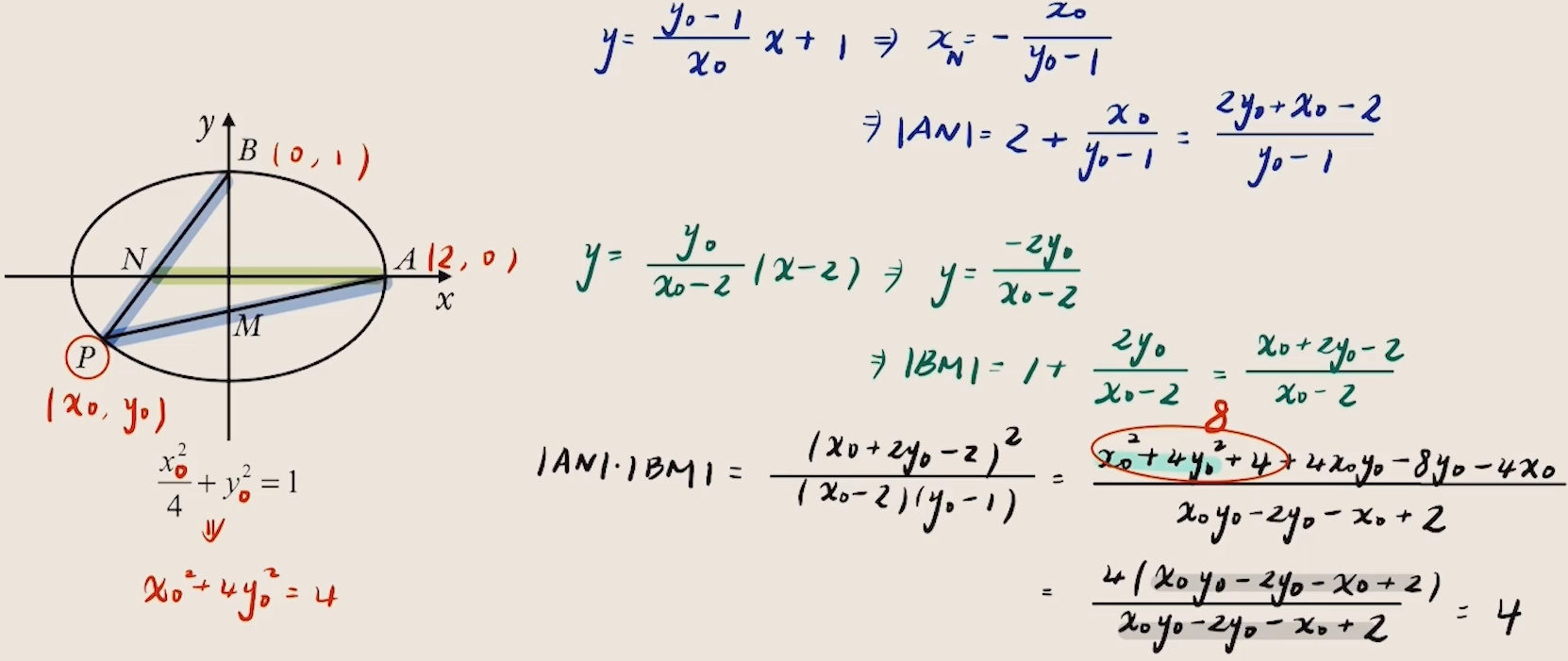
设直线方程的解题思路
设线的做题方法也差不多,但是考虑到计算难度,需要根据情况设出不同的直线表示式。如果直线有一定点在$y$轴上,设直线$y=kx+m$。定点在$x$轴上,设直线$x=\lambda y+m$。如果经过任意不在坐标轴的定点$(m,n)$,则设直线$y-n=k(x-m)$更加合适。
(注:前两种直线方程分别不能表示与$x$轴垂直和与$x$轴水平的直线,因此在有必要的情况下分类讨论。)
例题2(北京 2020):已知点 $A(-2,-1)$ 在椭圆上,过点 $B(-4,0)$的直线 $\iota$交椭圆$C:\frac{x^2}{8}+\frac{y^2}{2}=1$于点$M$,$N$,直线$MA,NA$分别交直线 $x=-4$ 于点$P,Q.$ 求$\frac{|PB|}{|BQ|}$的值.
解答过程:设点如图: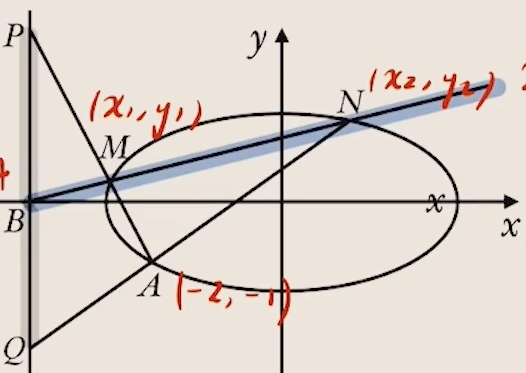
联立直线与椭圆得$$\begin{cases}x^{2}+4y^{2}-8=0\\x=xy-4&\end{cases}$$ 解得$$(\lambda y-4)^{2}+4y^{2}-8=0$$ 整理得$$(\lambda^{2}+4)y^{2}-8\lambda y+8=0$$ 即$$AM:y+1=\frac{y_{1}+1}{x_{1}+2}(x+2)$$ 所以$$y_p=\frac{-2y_1-x_1-y}{x_1+2}$$ 将$x=\lambda y-4$代入得$$y_p=\frac{-(\lambda+2)y_1}{\lambda y_1-2}$$ 同理得$$y_{Q}=\frac{-(\lambda+2)y_{2}}{\lambda y_{2}-2}$$ 所以$$\frac{|PB|}{|BQ|}=\left|\frac{y_{p}}{y_{Q}}\right|=\frac{y_{1}(\lambda y_{2}-2)}{(\lambda y_{1}-2)\cdot y_{2}}=\frac{\lambda y_{1}y_{2}-2y_{1}}{\lambda y_{1}y_{2}-2y_{2}}.$$ 这里的算式出现了二次项和一次项同时出现的形式。根据韦达定理:$x_1+x_2=-\frac{b}{a},x_1x_2=\frac{c}{a}$,直接代入无法消去$y_1,y_2$,必须将原式化为齐次式才可化简(简称非对称型韦达定理)。具体过程:$$\frac{y_{1}+y_{2}}{y_{1}\cdot y_{2}}=\frac{\frac{8\lambda}{\lambda^{2}+4}}{\frac{8}{\lambda^{2}+4}}\Rightarrow\frac{y_{1}+y_{2}}{y_{1}y_{2}}=\lambda$$ 即$$\lambda y_1y_2=y_1+y_2.$$ 由此便可得到$y_1y_2$和$y_1+y_2$的关系,继续代入上式得:$$\frac{|y_{2}-y_{1}|}{|y_{1}-y_{2}|}=1$$ 所以$\frac{|PB|}{|BQ|}$的值是1。
因时间关系,笔记只能写到这里了。更多的方法论,在明天(1.14)的文章中我会继续更新。
日常杂记:Google Forms VS. Microsoft Forms?
在某个博客里看到了Office Forms的链接,一下子刷新了我对于微软的印象。以前自己只是接触了一小下微软的表单系统,发现制作的过程处处都非常不方便只好放弃,那段时间一直用的是Google Forms。众所周知,Google的服务在中国都是被封锁的,这让没有VPN可用的许多人都被排除在外。我不堪问卷星的感人优化和抽奖骗局,因此还萌生过自建表格系统的想法,对于没性能没实力的我来说,结果当然失败。
这次仅仅是看到了表单前台的界面就非常的动心,话不多说,立刻就前去官网制作了一份关于友情链接提交的表单。使用流畅是必须的,反人类的设计也比较少,虽然填写者方面没问题,不过还是会影响制作的过程。唯一的缺憾是相对Google表单来说,Microsoft的表单并没有让用户提交文件和图片的设置项,我想如果可以让用户提交文档的话,使用的场景应该会更多元一些。
但是表单的其他功能亮点也非常明显,比如有和微软Win11一样的圆角设计风格,可调整和自定义背景图片并且自动适配主题色,能添加一些自带的背景音乐,可以导出不同形式的表单链接(包括嵌入代码和二维码图片),还有一大堆比较新且不同场景的模板可以用(这点Google也有,可是那些模板快老掉牙了)。总的来说这次的体验真的不错。不过接下来如何把表单推向大众,说服他们去填写,那确实是需要关心的一大事情。
Microsoft 365新工具体验
顺着表单工具,我也看了看Office 365系列的更多工具。Word、Excel、PowerPoint和OneDrive,Outlook都是基本,除此以外我还发现“Designer”、“Clipchamp”、“Reading Coach”三个神奇在线软件,接下来毫不犹豫地就开始尝试使用。
Designer一看就是个图像设计软件,里面貌似还带有AI绘图功能,实际的体验不知和Canva相比会如何,但目前来说推销内容和流畅程度还是胜过一筹。



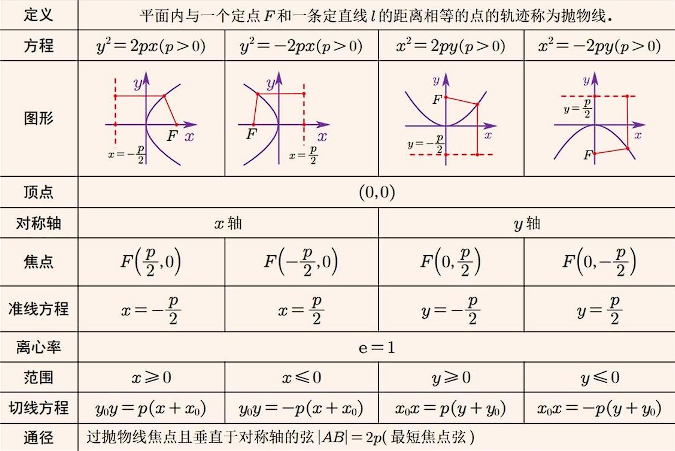
这个公式,好厉害wwwww 能不能插入LaTeX呢?
Google Forms体验不错,国内硬伤。